Gabor features

The idea behind Gabor feature calculation is filtering an image with an oriented texture element and treating a statistics calculated over pixels of the filter response image as a measure of the texture element’s abundance in the image. A set of \(k\) texture elements with unique calibrated direction and spatial frequency, called Gabor filter bank, is used to calculate a \(k\) -dimensional feature vector serving as a discriminating descriptor of the whole image. To dampen the bias of varying intensity range in an image, its feature vector is normalized with respect to a feature vector of an image produced with a equalizing filter.

Let \(I(x,y)\) be a real valued 2D image intensity function at Cartesian location \((x,y)\) . The oriented texture element is defined as a kernel of Gabor filter at location \((x,y)\). A Gabor kernel defined on a 2D domain of size \(n \times n\) is a product of Gaussian factor \(g\) and harmonic factor \(f\) :

\[\begin{split}h(x, y, \lambda, \theta, \psi, \sigma, \gamma) = g(x',y',\gamma,\sigma) \ f(x',\lambda,\psi) \\ = exp \Big(-\frac {x'^2+\gamma^2 y'^2} {2\sigma^2} \Big) \ exp \Big[ i \Big( \frac {2 \pi x'}{\lambda} + \psi \Big) \Big]\end{split}\]

where \(x,y \in \overline{1,n}\), \(x' = x \ \cos \ \theta + y \ \sin \ \theta\) and \(y' = -x \ sin \ \theta + y \ cos \ \theta\) .

\(\sigma\) is standard deviation of the Gaussian factor \(g\) playing the role of bandwidth controlling the overall size of the Gabor envelope. Larger bandwidth values increase the envelope allowing more periodic ridges while smaller values result in fewer ridges.

\(\theta\) is the angle of orientation of the normal to the major axis of the Gabor envelope. \(\theta=0\) corresponds to the vertical position of ridges of the harmonic factor.

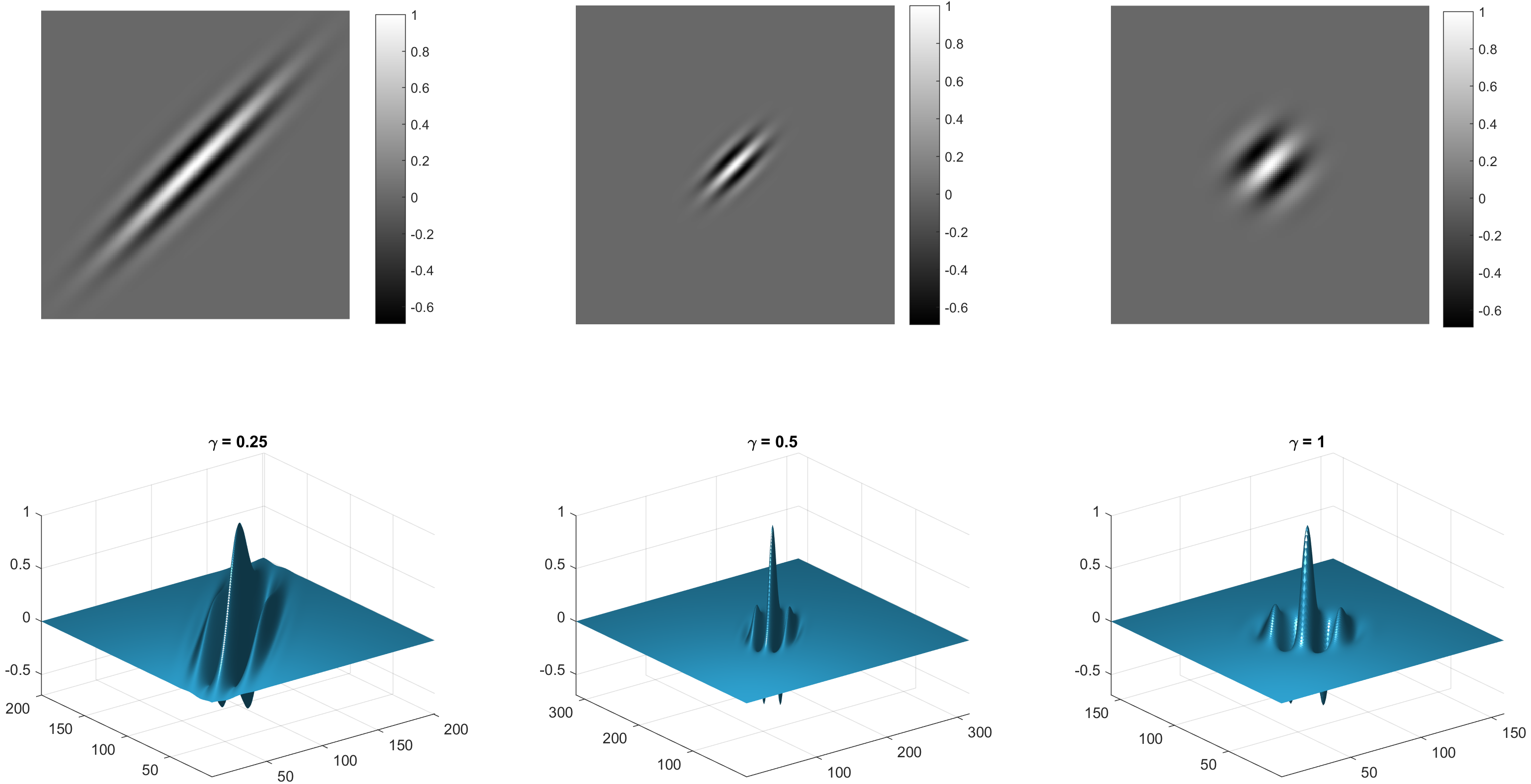
\(\gamma\) is the aspect ratio of the Gaussian factor \(g\).

The effect of varying \(\gamma\) at \(\theta=\frac{3}{4}\pi\) is shown below:

Parameters \(\lambda\) and \(\psi\) are the wavelength and phase shift of complex harmonic factor

\[f = exp \Big[ i(\frac {2 \pi x'}{\lambda} + \psi) \Big]\]

or equivalently

\[\begin{split}Re(f) = cos \Big[ 2 \pi (\frac {2 \pi x'}{\lambda} + \psi) \Big] \\ Im(f) = sin \Big[ 2 \pi (\frac {2 \pi x'}{\lambda} + \psi) \Big]\end{split}\]

In Nyxus implementation of the Gabor feature, parameters \(\lambda\) and \(\sigma\) are coupled in the form of parameter “sig2lam” playing the role of spatial bandwidth:

\[\textrm{sig2lam} = \frac {\sigma} {\lambda}\]

Tuning Gabor feature parameters is advised to start with tuning \(\frac {\sigma} {\lambda}\). There are multiple approaches to the tuning, for example, one based on maximizing the signal to noise ratio of the filter response image \(R(x,y)\) :

\[\textrm{SNR} = - \Big( \frac {\mu_R} {\sigma_R} \Big) ^2\]

where \(\mu_R\) and \(\sigma_R\) is the mean intensity and standard deviation of \(R\), respectively .

The filter response image \(R(x,y)\) is calculated by convolving the original image \(I(x,y)\) with Gabor filter \(g(x, y, \lambda, \theta, \psi, \sigma, \gamma)\) in the discrete domain:

\[R (x, y, \lambda, \theta, \psi, \sigma, \gamma) = \sum_{x'} \ \sum_{y'} \ I(x-x', y-y') \ h(x', y', \lambda, \theta, \psi, \sigma, \gamma)\]

Define a set of values \(C = \{ \lambda, \theta, \psi, \sigma, \gamma \}\) a filter configuration \(C\), and a set of configurations \(B = \{ C_1, C_2, ... C_k \}\) a filter bank \(B\). Nyxus implementation of Gabor filter banks requires that some parameters be shared by the filter bank per Gabor feature calculation: \(\psi=0\) and \(\sigma=const, \gamma=const\) while the other parameters can be user-specified as arrays of values. An example:

\[\begin{split}C = \{ {\lambda_1, \theta_1, \psi, \sigma, \gamma}, \\ {\lambda_2, \theta_1, \psi, \sigma, \gamma}, \\ {\lambda_3, \theta_1, \psi, \sigma, \gamma}, \\ {\lambda_4, \theta_1, \psi, \sigma, \gamma}, \\ {\lambda_1, \theta_2, \psi, \sigma, \gamma}, \\ {\lambda_2, \theta_2, \psi, \sigma, \gamma}, \\ {\lambda_3, \theta_2, \psi, \sigma, \gamma}, \\ {\lambda_4, \theta_2, \psi, \sigma, \gamma} \}\end{split}\]

Values of \(k\) -dimensional feature vector in Nyxus are calculated as scored ratios

\[r_i = \frac {R_i} {R_0}\]

of the ROI image \(I(x,y)\) convolved with Gabor high-pass filter kernels at various wavelengths and orientations to \(I(x,y)\) convolved with a low-pass Gabor kernel of wavelength \(f_0\) .

The score \(s\) is calculated as the number of pixels of the convolved image greater than some threshold \(r_0\):

\[s_i = \sum_{x} \ \sum_{y} r_i(x,y) : r_i(x,y)>r_0\]

Nyxus calculates the baseline filter response \(h_0\) as

\[h_0 = g(x',y',\gamma,\sigma) f(x',\lambda_0,\psi)\]

where

\[\lambda_0 = \pi / f_0\]

with respect to customizable parameter “f0”.

The following table presents customizable parameter of the Gabor feature and their default values:

Parameter	Nyxus CLI option	Default value
\(\lambda\)	–gaborfreqs	{1, 2, 4, 8, 16, 32, 64}
\(\gamma\)	–gaborgamma	0.1
\(\sigma / \lambda\)	–gaborsig2lam	0.8
\(n\)	–gaborkersize	16
\(f_0\)	–gaborf0	0.1
\(\theta\)	–gabortheta	45 (degrees)
\(r_0\)	–gaborthold	0.025